2023年成考专升本每日一练《高等数学一》10月4日专为备考2023年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、设y=x-2+3,则y'|x=1=()。
- A:3
- B:-3
- C:2
- D:-2
答 案:D
解 析:y'=(x-2+3)'=(x-2)'+3'=-2x-3=-2。
2、微分方程y'=2y的通解为y=()。
- A:
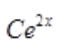
- B:
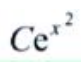
- C:
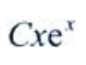
- D:
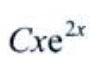
答 案:A
解 析:将方程y'=2y分离变量得,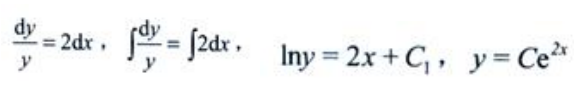 。
。
3、设y=f(x)为分段函数,x0为其分段点,且函数在x0处连续,则下列命题()正确。
- A:f(x)在点x0处必定可导
- B:f(x)在点x0处必定可微
- C:
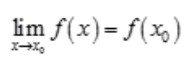
- D:

答 案:C
解 析:函数在x0处连续,即在x0处f(x)的左右极限存在且相等,所以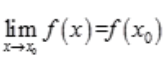 。
。
主观题
1、曲线y2+2xy+3=0上哪点的切线与x轴正向所夹的角为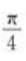 ?
?
答 案:解:将y2+2xy+3=0对x求导,得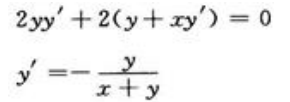 欲使切线与x轴正向所夹的角为
欲使切线与x轴正向所夹的角为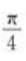 ,只要切线的斜率为1,即
,只要切线的斜率为1,即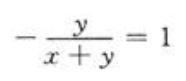 亦即x+2y=0,设切点为(x0,y0),则x0+2y0=0①
亦即x+2y=0,设切点为(x0,y0),则x0+2y0=0①
又切点在曲线上,即y02+2x0y0+3=0②
由①,②得y0=±1,x0=±2
即曲线上点(-2,1),(2,-1)的切线与x轴正向所夹的角为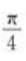 。
。
2、求微分方程y''-9y=0的通解
答 案:解:特征方程为r2-9=0,其特征根为r1=-3,r2=3,故通解为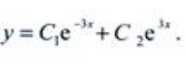 (C1,C2为任意常数)
(C1,C2为任意常数)
3、求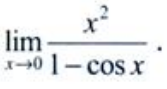
答 案:解:方法一:(洛必达法则)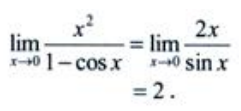 方法二:(等价无穷小)
方法二:(等价无穷小)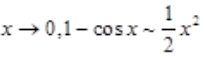
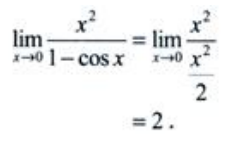
填空题
1、设y=(x+3)2,则y'=()。
答 案:2(x+3)
解 析: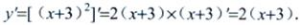
2、函数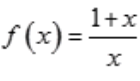 在[1,2]上符合拉格朗日中值定理的
在[1,2]上符合拉格朗日中值定理的 =_。
=_。
答 案:
解 析:由拉格朗日中值定理有 解得
解得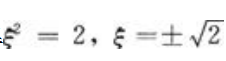 ,其中
,其中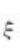 =-
=- (舍),得
(舍),得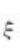 =
= 。
。
3、已知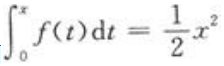 ,则
,则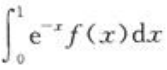 =()。
=()。
答 案: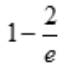
解 析: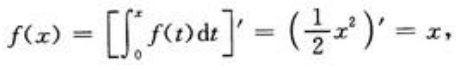
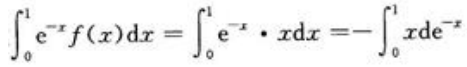
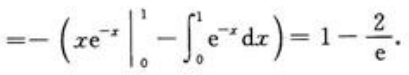
简答题
1、设函数z(x,y)由方程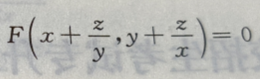 所确定
证明:
所确定
证明: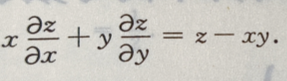
答 案: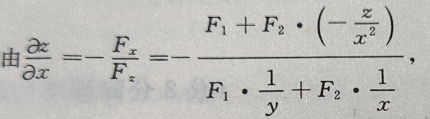
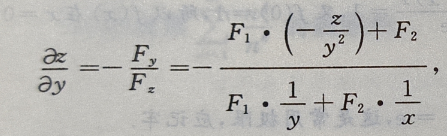 所以
所以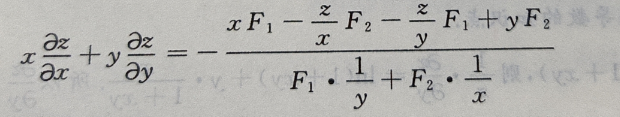
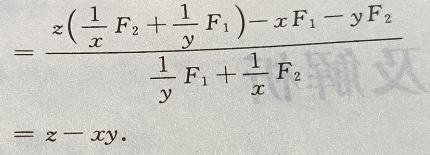
精彩评论