2023年高职单招每日一练《数学》10月18日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、设π/4cosa。（）  

答 案：对

解 析：一全正，二正弦，三正切，四余弦（口诀）但是在第一象限以π/4发现为基准，当a大于π/4时，sina>cosa，当a小于π/4时，sinacosa，是正确的

2、在比例尺1：4000的地图上，长度为5cm的公路实际长度为200m。（）  

答 案：对

解 析：设这条道路的实际长度为xcm，根据题意得5：x=1：4000 解得x=20000，20000cm=200m，故正确  

单选题

1、cos=（）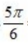  

• A：
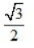
• B：
• C：1/2
• D：-1/2

答 案：B

解 析：运用诱导公式规律奇变偶不变，符号看象限cos5π/6＝cos(π/2+π/3)＝-sinπ/3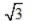＝-/2

2、长方形的一边长等于3a+2b，另一边比它大a-b，那么这个长方形的周长是()  

• A：14a+6b
• B：7a+3b
• C：10a+10b
• D：12a+8b

答 案：A

解 析：长方形的一边长等于3a+2b，另一边比他大a-b，则另一边长是3a+2b+a-b=4a+b，于是这个长方形的周长是：2（3a+2b+4a+b）=2（7a+3b)=14a+6b

多选题

1、列命题中正确的个数是(　　)  

• A：若a，b，c成等差数列，则a2，b2，c2一定成等差数列；
• B：若a，b，c成等差数列，则2a,2b,2c可能成等差数列；
• C：若a，b，c成等差数列，则ka＋2，kb＋2，kc＋2一定成等差数列；
• D：若a，b，c成等差数列，则1/a，1/b，1/c可能成等差数列．

答 案：BCD

解 析：对于A取a＝1，b＝2，c＝3,a2＝1，b2＝4，c2＝9，A错； 对于B，a＝b＝c，2a＝2b＝2c，B正确；对于C，∵a，b，c成等差数列，∴a＋c＝2b.∴(ka＋2)＋(kc＋2)＝k(a＋c)＋4＝2(kb＋2)，C正确；对于D，a＝b＝c≠0?1/a=1/b=1/c，D正确。综上可知选BCD。  

2、已知等差数列{a_n}的前n项和为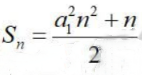，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

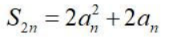
答 案：ABC

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、已知A(0,1),B(1,2),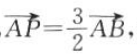则点P的坐标为（）  

答 案：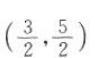

解 析：设点P的坐标为(x,y),则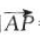=(x,y-1),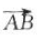=(1,1).因为所以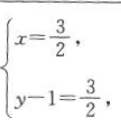  

2、直线y=-2x+b经过（3,2），则b=（）  

答 案：8

解 析：由题意得：将点（3,2）代入y=-2x+b得：2=-2x3+b，解得b=8