2023年高职单招每日一练《数学》10月21日专为备考2023年数学考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、方程x²+y²=9表示圆心在原点，半径为3的一个圆。（）  

答 案：对

2、已知函数f（x）的定义域为[-1，5]、在同一坐标系下，函数y=f（x）的图象与直线x=1的交点个数为（　　）  

答 案：对

解 析：∵f（x）的定义域为[-1，5]，而1∈[-1，5]，∴点（1，f（1））在函数y=f（x）的图象上。而点（1，f（1））又在直线x=1上，∴直线x=1与函数y=f（x）的图象至少有一个交点（1，f（1））。根据函数的定义知，函数是一个特殊的映射，即对于定义域[-1，5]中的任何一个元素，在其值域中只有唯一确定的元素f（1）与之对应，故直线x=1与y=f（x）的图象有且只有一个交点。

单选题

1、某人2000年1月1日到银行存入一年期定期存款a元，若年利率为x，按复利计算，到期自动转存，那么到2014年1月1日可取回款（）  

• A：a（1+r）¹⁴
• B：a（1+r）¹⁵
• C：a（1+r）¹³
• D：a+a（1+r）¹³

答 案：A

2、在等差数列中，a₁+a₉=10,则a₅的值为(   ).  

• A：5                                                                          
• B：6
• C：8                                                                          
• D：10

答 案：A

解 析：在等差数列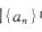由a₁+a₉=10可得2a₅=a₁+a₉=10,所以a₅=5 .故选A .

多选题

1、已知等差数列{a_n}的前n项和为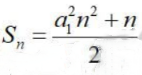，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
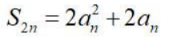
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

2、已知函数y=1/2sin2x则（）  

• A：函数最大值为2
• B：函数最大值为1/2
• C：周期
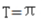
• D：周期

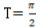
答 案：BC

解 析：A：sin2x最大值为1，则y=1/2sin2x的最大值为1/2，故A错B对。C：T=2π/W=2π/2=π，故C对D错

主观题

1、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、在30°的二面角的一个面内有一个点，它到另一个面的距离是10cm，这点到棱的距离是_____.

答 案：20cm

解 析：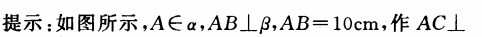

2、若不等式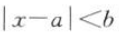的解集是(-2,8),则a,b分别是（）.

答 案：3,5

解 析：解不等式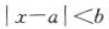得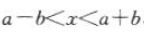,又因为其解集是(-2,8),所以a - b= - 2,a+b= 8,解得a=3,b=5 .